
Various symbols for function commands may also be shown on the display. Large-sized figures are often used to improve readability while using decimal separator (usually a point rather than a comma) instead of or in addition to vulgar fractions. Most basic calculators assign only one digit or operation on each button however, in more specific calculators, a button can perform multi-function working with key combinations.Ĭalculators usually have liquid-crystal displays (LCD) as output in place of historical light-emitting diode (LED) displays and vacuum fluorescent displays (VFD) details are provided in the section Technical improvements.

Scientific calculator displays of fractions and decimal equivalents InputĮlectronic calculators contain a keyboard with buttons for digits and arithmetical operations some even contain "00" and "000" buttons to make larger or smaller numbers easier to enter. By 2007, this had diminished to less than 0.05%. In 1986, calculators still represented an estimated 41% of the world's general-purpose hardware capacity to compute information. With the very wide availability of smartphones, tablet computers and personal computers, dedicated hardware calculators, while still widely used, are less common than they once were. As of 2016, basic calculators cost little, but scientific and graphing models tend to cost more. Graphing calculators can be used to graph functions defined on the real line, or higher-dimensional Euclidean space. Some calculators even have the ability to do computer algebra. For example, there are scientific calculators which include trigonometric and statistical calculations. In addition to general purpose calculators, there are those designed for specific markets. By the end of that decade, prices had dropped to the point where a basic calculator was affordable to most and they became common in schools.Ĭomputer operating systems as far back as early Unix have included interactive calculator programs such as dc and hoc, and calculator functions are included in almost all personal digital assistant (PDA) type devices, the exceptions being a few dedicated address book and dictionary devices. They became popular in the mid-1970s as the incorporation of integrated circuits reduced their size and cost. Modern electronic calculators vary from cheap, give-away, credit-card-sized models to sturdy desktop models with built-in printers. They later became used commonly within the petroleum industry (oil and gas). Pocket-sized devices became available in the 1970s, especially after the Intel 4004, the first microprocessor, was developed by Intel for the Japanese calculator company Busicom. The first solid-state electronic calculator was created in the early 1960s.
#Statistical calculations calcualtor portable
Ques: Find out the root mean square RMS of the given data set 1, 2, 3, 7, 8(3 marks)A modern scientific calculator with a dot matrix LCDĪn electronic calculator is typically a portable electronic device used to perform calculations, ranging from basic arithmetic to complex mathematics. Quest: Find out the root mean square RMS of the given data set 6, 5, 10, 3, 11 (3 marks) Ques: Find out the root mean square RMS of the given data set 6, 5, 4, 3, 7 (3 marks) Ques: Find out the root mean square RMS of the given data set 6, 5, 4, 2, 7 (3 marks) Ques: Find out the root mean square RMS of the given data set 2, 3, 5, 7, 11 (3 marks) Step1: Calculate the squares of all the values. Ques: Find out the root mean square RMS of the given data set 1, 3, 5, 7, 9 (3 marks) Step 3: Finally, calculate the average's square root. Step 2: Figure out the average of the squares that are obtained.
Step 1: Calculate the squares of all the values. The following are the steps to find the root mean square for a given set of values: The RMS value of various waveforms can also be computed without the use of calculus. The RMS value of a continuous function can be approximated by obtaining the RMS of a sequence of evenly spaced entities. The RMS of a periodic function is always equal to the RMS of the single period of the function.
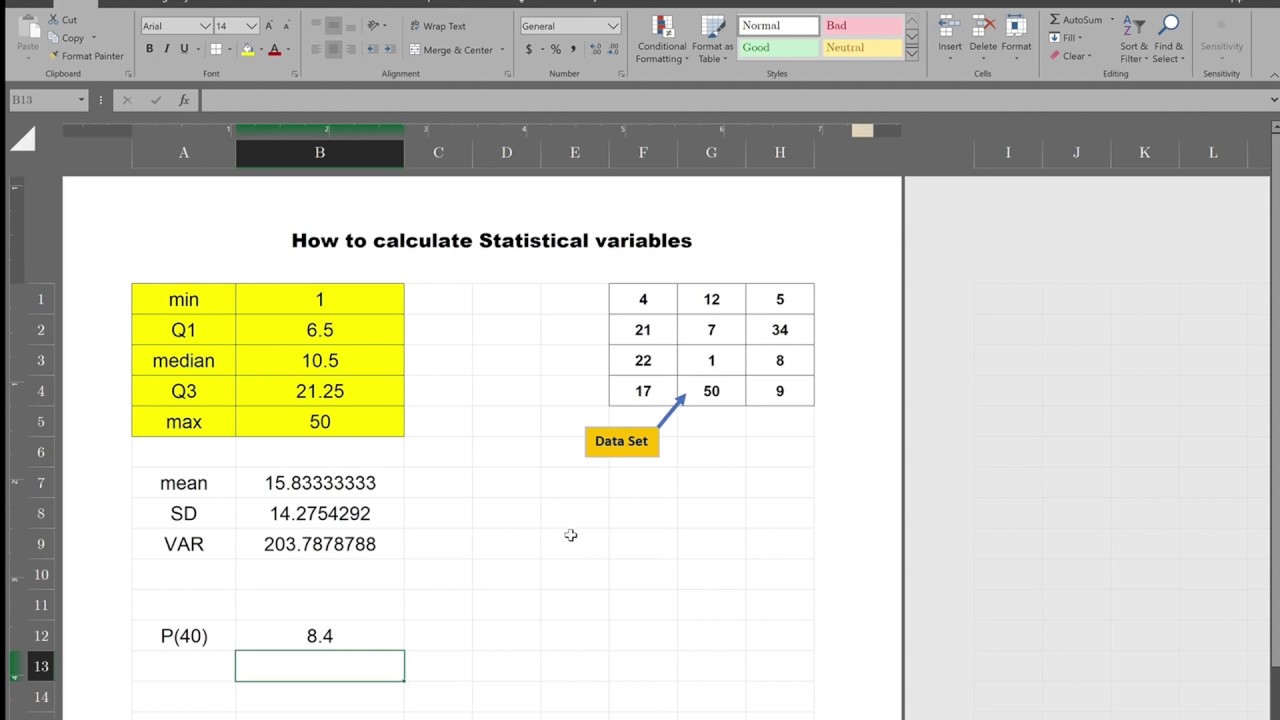
The following is the formula for a continuous function f(t) defined for the interval T1 ≤ t ≤ T2: The RMS of a set of n values involving is given by: To calculate the RMS value of a set of data values, use the Root Mean Square formula below. The RMS or the root mean square of a set of numbers is the square of the arithmetic mean or the square of the function that defines the continuous waveform.


 0 kommentar(er)
0 kommentar(er)
